Estabilidad de taludes

Estabilidad de taludes: Por talud se entiende una porción de vertiente natural cuyo perfil original ha sido modificado con intervenciones artificiales relevantes con respecto a la estabilidad. Por derrumbe se entiende una situación de inestabilidad que concierne vertientes naturales y comprende considerables espacios de terreno.

Introducción al análisis de estabilidad
Para resolver un problema de estabilidad es necesario tener en cuenta las ecuaciones de campo y los vínculos constitutivos. Las primeras tienen que ver con el equilibrio, mientras que los vínculos describen el comportamiento del terreno. Tales ecuaciones son particularmente complejas ya que los terrenos son sistemas multifase, que se pueden convertir en sistemas monofase solo en condiciones de terreno seco, o de análisis en condiciones drenadas.
En la mayor parte de los casos nos encontramos con suelos que además de saturados, son también bifase, lo que vuelve notoriamente complicado el análisis de las ecuaciones de equilibrio. Además es prácticamente imposible definir una ley constitutiva de validez general, ya que los terrenos presentan un comportamiento no-lineal y aún en caso de pequeñas deformaciones, son anisótropos y su comportamiento depende no solo del esfuerzo desviador, sino también del normal. Para enfrentar estas dificultades se introducen hipótesis que ayuden a simplificar:

1. Se usan leyes constitutivas simplificadas: modelo rígido perfectamente plástico. Se asume que la resistencia del suelo se expresa únicamente con los parámetros cohesión (c) y ángulo de rozamiento (φ), constantes para el terreno y característicos del estado plástico. Por tanto, se considera válido el criterio de rotura de Mohr-Coulomb.

2. En algunos casos se satisfacen solo en parte las ecuaciones de equilibrio.

Método del equilibrio límite (LEM)
El método del equilibrio límite consiste en estudiar el equilibrio de un cuerpo rígido, constituido por el talud y por una superficie de deslizamiento de cualquier forma (línea recta, arco circular, espiral logarítmica). Con tal equilibrio se calculan las tensiones de corte (τ) y se comparan con la resistencia disponible (τ_f), calculada según el criterio de rotura de Coulomb: De tal comparación deriva la primera indicación de estabilidad, con el coeficiente de seguridad:

F=τ_f /τ

Entre los métodos del equilibrio último hay algunos que consideran el equilibrio global del cuerpo rígido (Culman) mientras que otros, por falta de homogeneidad, dividen el cuerpo en rebanadas y consideran el equilibrio de cada una (Fellenius, Bishop, Janbu, etc.).

 

A continuación se discuten los métodos del equilibrio último de las rebanadas.

Método de las rebanadas
La masa susceptible al deslizamiento se subdivide en un número conveniente de rebanadas. Si el número de rebanadas es igual a n, el problema presenta las siguientes incógnitas:

• n valores de las fuerzas normales N_i en la base de cada rebanada;
• n valores de las fuerzas de corte en la base de la rebanada T_i;
• (n-1) fuerzas normales E_i en la conexión de las rebanadas;
• (n-1) fuerzas tangenciales X_i en la conexión de las rebanadas;
• n valores de la coordenada del punto de aplicación de las E_i;
• (n-1) valores de la coordenada del punto de aplicación de las X_i;
• una incógnita constituida por el factor de seguridad F.

En total las incógnitas son (6n-2).
Mientras las ecuaciones a disposición son:

• ecuaciones de equilibrio de momentos n;
• ecuaciones de equilibrio en la traslación vertical n;
• ecuaciones de equilibrio en la traslación horizontal n;
• ecuaciones del criterio de rotura n.

Total número de ecuaciones 4n.

El problema es estáticamente indeterminado y el grado de indeterminación es igual a:

i=(6n-2)-4n=2n-2

El grado de indeterminación se reduce a (n-2). Al asumir que N_i se aplica en el punto medio de la franja, esto equivale a crear la hipótesis de que las tensiones normales totales están distribuidas uniformemente. Los diferentes métodos que se basan en la teoría del equilibrio límite se diferencian por el modo en que se eliminan las (n-2) indeterminaciones.

Método de Fellenius  (1927)
Con este método (válido solo para superficies de deslizamiento circulares) se pasan por alto las fuerzas entre las franjas, por lo tanto las incógnitas se reducen a:

• n valores de las fuerzas normales N_i;
• n valores de las fuerzas de corte T_i;
• 1 factor de seguridad.

Incógnitas (2n+1). Las ecuaciones disponibles son:

• n ecuaciones de equilibrio traslación vertical;
• n  ecuaciones del criterio de rotura;
• ecuación de equilibrio de momentos global.

 

F={Σ_ì[c_i·l_i+(W_i·cosα_i-u_i·l_i)·tanφ_i}/(Σ_ì·sinα_i)

Esta ecuación es fácil de resolver pero se ha visto que da resultados conservadores (factores de seguridad bajos) especialmente para superficies profundas.

Método de Bishop  (1955)
Con este método se toman en cuenta todas las fuerzas actuantes en los bloques. Fue el primero en describir los problemas relacionados con los métodos convencionales.
Las ecuaciones usadas para resolver el problema son:

Σ F_y=0  Σ M₀=0  Criterio de rotura

F={Σ_ì[c_i·b_i+(W_i-u_i·b_i+ΔX_i)·tanφ_i]·[secα_i/(1+tanα_i·tanφ_i/F)]}/(Σ_ìW_i·sinα_i)

Los valores de F y de ΔX que satisfacen esta ecuación dan una solución rigurosa al problema. Como primer aproximación conviene plantear ΔX = 0 e iterar para el cálculo del factor de seguridad. Este procedimiento se conoce como método de Bishop ordinario y los errores con respecto al método completo son de alrededor de un 1 %.

Método de  Janbu (1967)
Janbu extendió el método de Bishop a superficies de deslizamiento de cualquier forma. Cuando se tratan superficies de deslizamiento de cualquier forma el brazo de las fuerzas cambia (en el caso de las superficies circulares queda constante e igual al radio), por este motivo es mejor valorar la ecuación del momento respecto al ángulo de cada bloque.

F={Σ_ì[c_i·b_i+(W_i-u_i·b_i+ΔX_i)·tanφ_i]·[sec^(2)α_i/(1+tanα_i·tanφ_i/F)]}/(Σ_ìW_i·tanα_i)

Acciones en la i-ésima rebanada según las hipótesis de Janbu y representación de la totalidad de la masa

Asumiendo ΔX_i = 0 se obtiene el método ordinario. Janbu propuso además un método para la corrección del factor de seguridad obtenido con el método ordinario según lo siguiente:

F_corretto=f₀·F

Donde  f₀ depende de la geometría y de los parámetros geotécnicos y esto se puede encontrar en tablas y gráficos. Esta corrección es muy confiable para taludes poco inclinados.

Método de Bell  (1968)
Las fuerzas agentes sobre  el cuerpo resbaladizo incluyen el peso efectivo del terreno, W, las fuerzas sísmicas pseudo estáticas horizontales y verticales K_x·W e K_y·W, las fuerzas horizontales y verticales X y Z aplicadas externamente al perfil del talud, en fin, el resultado de los esfuerzos totales normales y  σ e τ agentes en la potencial superficie de deslizamiento.

El esfuerzo total normal puede incluir un exceso de presión de los poros u que se debe especificar con la introducción de los parámetros de fuerza eficaz. Prácticamente este método se puede considerar como una extensión del método del círculo de rozamiento en secciones homogéneas anteriormente descrito por Taylor. De acuerdo con la ley de la resistencia de Mohr-Coulomb en términos de tensión efectiva, la fuerza de corte agente en la base de la i-ésima rebanada está dada por:

 

T_i=[c_i·L_i+(N_i-u_ci·L_i)·tanφ_i]/F

Donde:

F = factor de seguridad;
c_i = cohesión eficaz (o total) en la base de la i-ésima rebanada;
φ_i  = ángulo de rozamiento eficaz (= 0 con la cohesión total) en la base de la i-ésima rebanada;
L_i  = longitud de la base de la i-ésima rebanada;
u_ci  = presión de los poros en el centro de la base de la i-ésima rebanada.

 

El equilibrio se da igualando a cero la suma de las fuerzas horizontales, la suma de las fuerzas verticales y la suma de los momentos con respecto al origen. Se adopta la siguiente asunción en la variación de la tensión normal agente en la potencial superficie de deslizamiento:

σ_{ci=[C1·(1-Kz)·(Wi·cosαi)/Li]+C2·f(xci,yci,zci)}

Donde el primer término de la ecuación incluye la expresión:

W_i·cosα_i/L_i= valor del esfuerzo normal total asociado al método ordinario de las rebanadas

El segundo término de la ecuación incluye la función:

f=sin2π·[(x_n-x_ci)/(x_n-x₀)]

Donde  x₀ y x_n son, respectivamente, las abscisas del primer y del último punto de la superficie de deslizamiento, mientras x_ci representa la abscisa del punto medio de la base de la i-ésima rebanada.
Una parte sensible de reducción del peso asociada a una aceleración vertical del terreno K_y g se puede transmitir directamente a la base y esto se incluye en el factor (1 – K_y).
El esfuerzo normal total en la base de una rebanada está dado por:

N_i= σ_ci ·L_i

La solución de las ecuaciones de equilibrio se consigue resolviendo un sistema lineal de tres ecuaciones, las cuales se obtienen multiplicando las ecuaciones de equilibrio por el factor de seguridad F , sustituyendo la expresión de N_i  y multiplicando cada término de la cohesión por un coeficiente arbitrario C₃. Con el fin de iniciar una solución iterativa, se puede usar cualquier par de valores del factor de seguridad dentro de una estimación físicamente razonable.
El número necesario de iteraciones depende tanto de la estimación inicial como de la precisión deseada para la solución; normalmente el proceso converge rápidamente.

Método de  Sarma (1973)
El método de Sarma es un simple pero esmerado método para el análisis de estabilidad de taludes que permite determinar la aceleración sísmica horizontal necesaria para que la masa de terreno, delimitada por la superficie de deslizamiento y por el perfil topográfico, alcance el estado de equilibrio límite (aceleración crítica K_c) y, al mismo tiempo, permite obtener el factor de seguridad obtenido como con los otros métodos comunes de la geotecnia.
Se trata de un método basado en el principio del equilibrio límite y de las franjas. Por lo tanto se considera el equilibrio de una masa potencial de terreno en deslizamiento subdividida en n franjas verticales de espesor suficientemente pequeño como para asumir que el esfuerzo normal Ni obra en el punto medio de la base de la franja.
Las ecuaciones a considerar son:

• La ecuación de equilibrio en la traslación horizontal de cada rebanada;
• La ecuación de equilibrio en la traslación vertical de cada rebanada;
• La ecuación de equilibrio de momentos.

Condiciones de equilibrio en la traslación horizontal y vertical:

N_i·cosα_i+T_i·sinα_i=W_i-ΔX_i
T_i·cosα_i-N_i·sinα_i=KW_i-ΔE_i

Además se asume que en ausencia de fuerzas externas en la superficie libre se tiene:

Σ ΔE_i = 0
Σ ΔX_ì  = 0

Donde E_i y X_i representan, respectivamente, las fuerzas horizontales y verticales en la i-ésima cara de la rebanada genérica i. La ecuación de equilibrio de momentos se escribe seleccionando como punto de referencia el baricentro del cúmulo; de manera que, después de haber efectuado una serie de posiciones y transformaciones trigonométricas y algebraicas, en el método de Sarma la solución del problema se obtiene resolviendo dos ecuaciones:

Acciones en la i-ésima rebanada, método de Sarma

Σ ΔX_ì·tan(ψ_i– α_i)+Σ ΔE_i=Σ Δ_i-KW_i

Σ ΔX_ì·[(y_mi-y_G)·tan(ψ_i– α_i)+(x_mi-x_G)]=Σ W_ì ·(x_mi-x_G)+Σ Δ_i-(y_mi-y_G)

Pero el enfoque de solución, en este caso, está completamente invertido: el problema en efecto requiere encontrar un valor de K (aceleración sísmica) correspondiente a un determinado factor de seguridad; y en particular, encontrar el valor de la aceleración K correspondiente al factor de seguridad F = 1, o sea la aceleración crítica.
Se tiene por lo tanto:

K=Kc      Aceleración crítica si F=1
F=Fs      Factor de seguridad en condiciones estáticas si  K=0

La segunda parte del problema del Método de Sarma es encontrar una distribución de fuerzas internas X_i y E_i tal que permita verificar el equilibrio de la rebanada y el equilibrio global del macizo, sin violar el criterio de rotura.
Se ha encontrado que una solución aceptable al problema se puede obtener asumiendo la siguiente distribución de las fuerzas X_i  :

ΣΔX_ì=λ·ΔQ_ì=λ·(Q_ì+1-Q₁)

Donde Q_i es una función conocida, donde se toman en cuenta los parámetros geotécnicos promedio en la i-ésima cara de la rebanada i, y l representa una incógnita. La solución completa del problema se obtiene por lo tanto, después de algunas iteraciones, con los valores de K_c, l y F, que permiten obtener también la distribución de las fuerzas entre las franjas.

 Método de Spencer  (1967)
El método se basa en el supuesto de que:

1. Las fuerzas de conexión a lo largo de las superficies de división de cada rebanada están orientadas paralelamente entre sí e inclinadas con respecto a la horizontal de un ángulo θ;
2. Todos los momentos son nulos Mi =0 i=1…..n

Básicamente el método satisface todas las ecuaciones de la estática y equivale al método de Morgenstern y Price cuando la función f(x) = 1. Imponiendo el equilibrio de momentos respecto al centro del arco descrito por la superficie de deslizamiento se tiene:

1) ΣQ_ì·R·cos(α-θ)=0

Donde:

Q_ì=0

fuerza de interacción entre las rebanadas;

R = radio del arco circular;
θ = ángulo de inclinación de la fuerza Q_i respecto a la horizontal.

Imponiendo el equilibrio de las fuerzas horizontales y verticales se obtiene respectivamente:

Σ(Q_ì·cosθ)=0
Σ(Q_ì·senθ)=0

Asumiendo las fuerzas Q_i  paralelas entre sí, se puede también escribir:

2) ΣQ_ì=0

Q_ì={c/F_s·(W·cosα-γ_w·h·l·secα)·tanα/F_s-W·sinα}/{cos(α-θ)·[(F_s+tanφ·tan(α-θ)]/F_s}

El método propone el cálculo de dos coeficientes de seguridad: el primero (F_sm) se obtiene de 1), ligado al equilibrio de momentos; el segundo (F_sf) dalla 2) de 2) ligado al equilibrio de fuerzas. En práctica se procede resolviendo la 1) y la 2) para un intervalo dado de valores del ángulo θ, considerando como valor único del coeficiente de seguridad aquel para el cual se obtiene:

F_sm=F_sf

Método de Morgenstern e Price (1965)
e establece una relación entre los componentes de las fuerzas de interconexión de tipo X = λ f(x)E, donde  λ es un factor de escala y f(x), es la función de la posición de E y de  X, que define una relación entre las variaciones de la fuerza X y de la fuerza E dentro la masa deslizante. La función f(x) se escoge arbitrariamente (constante, sinusoide, semisinusoide, trapecio, fraccionada) e influye poco sobre el resultado, pero se debe verificar que los valores obtenidos de las incógnitas sean físicamente aceptables.

La particularidad del método es que la masa se subdivide en franjas infinitesimales, a las cuales se aplican las ecuaciones de equilibrio en la traslación horizontal y vertical y de rotura en la base de las franjas. Se llega a una primer ecuación diferencial que une las fuerzas de conexión incógnitas E, X, el coeficiente de seguridad Fs, el peso de la franja infinitésima dW el resultado de las presiones neutras en la base dU.

Se obtiene la llamada “ecuación de las fuerzas”:

c’·(α/F_s)+tanφ’·[(dW/dx)-(dX/dx)-tanα(dE/dx)-secα·(dU/dx)]=(dE/dx)-tanα·[(dX/dx)-(dW/dx)]

Acciones en la i-ésima rebanada según las hipótesis de Mongester y Price y representación del conjunto

Una segunda ecuación, llamada “ecuación de los momentos”, se escribe imponiendo la condición de equilibrio a la rotación respecto a la base:

X=d(E_γ)/dx-γ·dE/dx

Estas dos ecuaciones se extienden por integración a toda la masa deslizante.
El método de cálculo satisface todas las ecuaciones de equilibrio y se aplica a superficies de cualquier forma, pero implica necesariamente el uso de un ordenador.

Método de Zeng e Liang (2002)
Con Zeng y Liang se efectuaron una serie de análisis paramétricos en un modelo bidimensional, desarrollado según los elementos finitos, que recrea el caso de pilotes en un terreno en movimiento (drilled shafts). El modelo bidimensional reproduce una franja de terreno de espesor 1 y supone che el fenómeno se de en condiciones de deformación plana en dirección paralela al eje de los pilotes.
Dicho modelo ha sido utilizado para investigar la influencia que tienen en la formación del efecto arco, algunos parámetros como el intereje entre pilotes, el diámetro y la forma de los mismos y las propiedades mecánicas del suelo. En la relación entre interejes y el diámetro de los pilotes (s/d), los autores identifican el parámetro adimensional determinante en la formación del efecto arco.
El problema resulta ser estáticamente indeterminado, con un grado de indeterminación igual a (8n-4), sin embargo es posible obtener una solución reduciendo el número de incógnitas y asumiendo hipótesis simplificadoras, con el fin de determinar el problema.

Los supuestos que determinan el problema son:

-K_y se asumen como horizontales con el fin de reducir el número total de incógnitas de (n-1) a (7n-3);
-Las fuerzas normales en la base de la banda actúan en el punto medio, reduciendo las incógnitas  de n a  (6n-3);
-La posición de los empujes laterales está a un tercio de la altura promedio de la inter rebanada y reduce las incógnitas de (n-1) a (5n-2);
-Las fuerzas (Pi-1) y Pi  se asumen como paralelas a la inclinación de la base de la franja (αi), reduciendo el número de incógnitas de (n-1) a (4n-1);
-Se asume un único límite elástico para todas las franjas, reduciendo las incógnitas  de (n) a  (3n-1).

El número total de incógnitas se reduce por lo tanto a (3n) y para calcularlas se usa el factor de transferencia de carga. Además se debe tener en cuenta que la fuerza de estabilización transmitida al terreno en el lado externo de los pilotes se reduce en una cantidad R, llamado factor de reducción, calculado como a continuación:

R=[1/(s/d)]+{1-[1/(s/d)]}·R_p

El factor R depende por lo tanto del cociente entre el intereje de los pilotes y el diámetro de los mismos y del factor R_p que toma en cuenta el efecto arco.

Estimación de la acción sísmica
Para verificar la estabilidad de taludes con acción sísmica se usa el método pseudo-estático. Para terrenos que con una carga cíclica puedan desarrollar presiones intersticiales elevadas, se considera un aumento porcentual de las presiones neutras que toma en cuenta este factor de pérdida de resistencia.
Para evaluar la acción sísmica se consideran las siguientes fuerzas:

F_H=K_x·W
F_V=K_y·W

Donde:

• F_H and  F_V respectivamente, el componente horizontal y vertical la fuerza de inercia aplicada al baricentro de la rebanada;
• W peso de la rebanada;
• K_x coeficiente sísmico horizontal;
• K_y coeficiente sísmico vertical.

Búsqueda de la superficie de deslizamiento crítica
En presencia de suelos homogéneos no se dispone de métodos para individuar la superficie de deslizamiento crítica y se debe examinar un elevado número de superficies potenciales.
En caso de superficies de forma circular la búsqueda se hace más sencilla, ya que después de haber colocado una malla centros de m líneas y n columnas, se examinan todas las superficies cuyo centro sea el nudo genérico de la malla mn con radio variable dentro un determinado rango de valores, de forma tal que se examinan superficies cinemáticamente admisibles.

Estabilidad de taludes utilizando pilotes
stresses at the top (passive pile – active soil) and resistive in the area below ground level (active pile – passive soil). From this interference between “barrier” and moving mass, are developed stabilizing actions that must pursue the following objectives:Los pilotes ayudan a aumentar la resistencia al corte en ciertas superficies de deslizamiento. La operación puede ser el resultado de una estabilidad ya establecida, donde se conoce la superficie de deslizamiento, o bien de forma preventiva, se puede proyectar según hipotéticas superficies de rotura que responsablemente, se asumen como las más probables. En ambos casos, se opera considerando una masa de terreno en movimiento sobre un cúmulo estable en el cual se atesta la alineación de pilotes.

El terreno de ambas zonas tiene una influencia distinta sobre el elemento uniaxial (pilote): solicitaciones en la parte superior (pilote pasivo – terreno activo) y resistencia en la zona inferior (pilote activo – terreno pasivo). De esta interferencia, entre “barrera” y masa en movimiento derivan las acciones estabilizadoras, las cuales deben perseguir los siguientes objetivos:

1. conferir al talud un coeficiente de seguridad mayor del que posee;
2. ser absorbidas por la estructura garantizando su integridad (las tensiones internas, derivadas de las solicitaciones máximas transmitidas a las diferentes secciones de cada pilote, deben ser inferiores a las admisibles del suelo) y resultar inferiores a la carga última que soporta el terreno calculada, lateralmente considerando la iteración (pilote-terreno).

Carga última de la interacción entre los pilotes y el terreno lateral
En los tipos de terreno cuyo comportamiento no es de tipo homogéneo, las deformaciones en la zona de contacto no están relacionadas entre sí. Por lo tanto al no poder asociar el suelo a un modelo de comportamiento perfectamente elástico (hipótesis que se puede asumir con materiales rocosos poco fracturados), generalmente se procede suponiendo que el movimiento de masa se encuentre en su estado inicial y que el terreno adyacente a los pilotes esté en la fase máxima consentida de plastificación, más allá de  la cual podría suceder que el material se deslice a través de la cortina de pilotes.

 

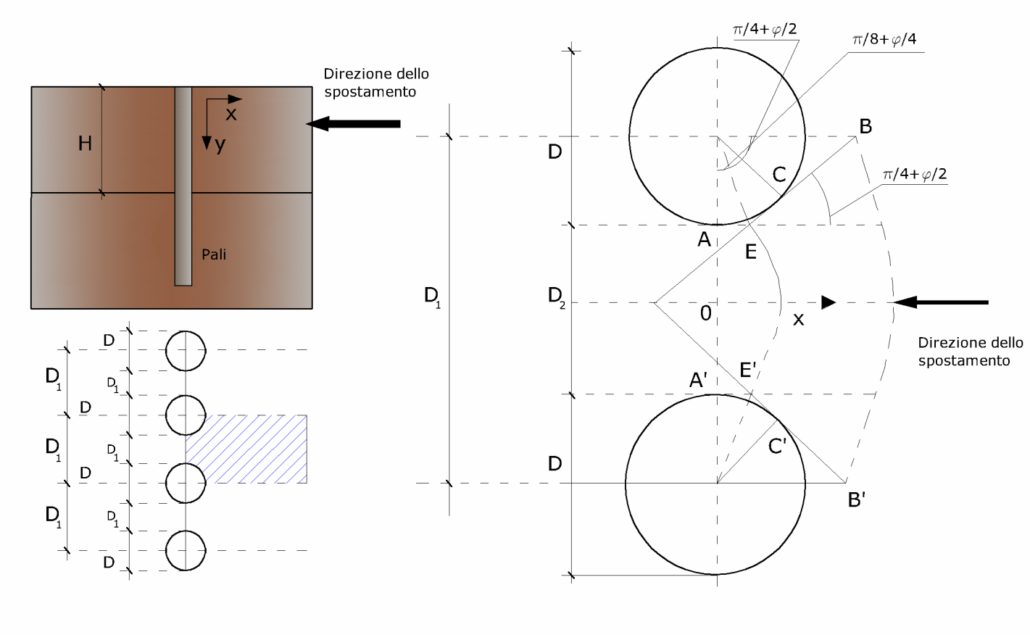Estableciendo además que la carga absorbida por el terreno sea igual a la de la condición límite hipotética y que entre dos pilotes consecutivos, como consecuencia del empuje activo, se instaure una especie de efecto arco, los autores T. Ito y T. Matsui (1975) obtuvieron la relación que permite determinar la carga última. Esto se logra refiriéndose al esquema estático diseñado en la figura anterior y a las hipótesis citadas.

• Bajo la acción del empuje activo del terreno se forman dos superficies de deslizamiento localizadas en las líneas AEB y A’E’B
• Las direcciones EB y E’B’ forman los siguientes ángulos con el eje x: +(45 + φ/2) e –(45 + φ/2) respectivamente
• El volumen del terreno, comprendido en la zona delimitada por los vértices AEBB’E’A’ tiene un comportamiento plástico, y por lo tanto se puede aplicar el criterio de ruptura de Mohr-Coulomb.
• La presión activa del terreno actúa en el plano A-A’;
• Los pilotes poseen una elevada rigidez a flexión y corte.

Dicha expresión, referida a la profundidad genérica Z, con respecto a un espesor de terreno unitario, es la siguiente:

P(Z)=C·D₁·(D₁/D₂)^(k₁)·{1/[(N_φ·tanφ)·(e^(k₂)-2(N_φ)^(0.5)·tanφ-1)]}-C·[D₁·k₃-D₂/(N_φ)^(0.5)+γ·Z/{N_φ-[D₁·(D₁/D₂)^(k₁)·e^(k₂)-D₂]}

Donde:

C = cohesión terreno;
φ = ángulo de rozamiento terreno;
γ = peso específico terreno;
D₁ = intereje entre pilotes;
D₂ = espacio libre entre dos pilotes consecutivos;
N_φ = tag²(π/4 + φ/2)

K₁=N_φ^(0.5)·tanφ+N_φ-1
K₂=[(D₂-D₁)/D₂]·N_φ·tan(π/8 + φ/4)
K₃=[2·tanφ+2·N_φ^(0.5)+1/N_φ^(0.5)]/[N_φ^(0.5)·tanφ+N_φ-1]

La fuerza total, con respecto a un estrato de terreno en movimiento de espesor H, se obtiene integrando la expresión anterior.
En presencia de terrenos granulosos (condición drenada), en los cuales se pueden asumir C = 0, la expresión se convierte en:

P(Z)=[0.5·γ·H^(2)]/{N_φ[D₁·(D₁/D₂)^(k₁)·e^(k₂)-D₂]}

Con terrenos cohesivos (condición no drenada), con  φ = 0 y C ≠ 0, se tiene:
P(Z)=C·{D₁·[3·ln(D₁/D₂)+(D₁-D₂)/(D₂)·tanπ/8]-2·(D₁-D₂)}+γ·z·(D₁-D₂)
P=ſ_0,HP(z)·dz
P(Z)=C·H·{D₁·[3·ln(D₁/D₂)+(D₁-D₂)/(D₂)·tanπ/8]-2·(D₁-D₂)}0.5·γ·H^(2)·(D₁-D₂)

El dimensionado de la cortina de pilotes que, como ya se ha mencionado, debe conferir al talud un incremento del coeficiente de seguridad y garantizar la integridad del mecanismo pilote-terreno, es bastante problemático. De hecho, dada la complejidad de la expresión de la carga P, que se ve influenciada por varios factores asociados sea a las características mecánicas del terreno que a la geometría de la estructura, no es fácil llegar a la solución más conveniente con una sola elaboración. Para alcanzar el objetivo es necesario realizar varios intentos con la finalidad de:

• Encontrar en el perfil topográfico del talud, una posición que pueda garantizar, en igualdad de condiciones, una mejor distribución de coeficientes de seguridad
• Determinar la colocación de los pilotes, caracterizada por la relación entre interejes y distancia entre los pilotes (D2/D1), que permite aprovechar al máximo la resistencia del complejo pilote-terreno. Por experiencia se ha comprobado que, excluyendo los casos límites (D2 = 0 P→ ∞ e D2 = D1 P→ valor mínimo), los valores más adecuados son aquellos para los cuales tal relación está comprendida entre 0,60 y 0,80;
• Evaluar la posibilidad de introducir más filas de pilotes y, en caso afirmativo, evaluar para las filas sucesivas, la posición que da más garantías en términos de seguridad y de ahorro de materiales;
• Adoptar el tipo de vínculo adecuado para obtener una distribución más regular de las solicitaciones. Por experiencia se ha constatado que el que alcanza mejor dicho objetivo es el vínculo que impide la rotación de la cabeza del pilote.

Método de la carga última de Broms
En caso de que la carga del pilote sea ortogonal al eje, configuración que se da cuando un pilote impide el movimiento de una masa en derrumbe, la resistencia puede quedar a cargo de su carga última horizontal.
Broms analiza el problema de cálculo de la carga última horizontal tanto para medios cohesivos como no cohesivos. Su método de cálculo se basa en algunas hipótesis simplificadoras con respecto a la reacción que ejerce el terreno por unidad de longitud de pilote en condiciones límite y también toma en cuenta la resistencia a la rotura del pilote (Momento de plastificación).

Elementos de Refuerzo
Los refuerzos son elementos horizontales y su aplicación aumenta la resistencia del terreno al desplazamiento.
Si el elemento de refuerzo interseca la superficie de desplazamiento, entonces la fuerza de resistencia que proporciona entra en la ecuación de equilibrio de cada rebanada; en caso contrario el elemento de refuerzo no tiene influencia alguna en la estabilidad.

Las comprobaciones internas tienen como objetivo estimar el nivel de estabilidad del terreno reforzado; los cálculos permiten la verificación de la rotura del elemento de refuerzo por tracción y la verificación del arrancamiento (Pullout).
El parámetro que suministra la resistencia a tracción del refuerzo, TAllow, se calcula partiendo de la resistencia nominal del material con el que ha sido realizado el mismo, reducido con coeficientes adecuados que tengan en cuenta la agresividad del terreno, el daño por efecto creep y el daño por instalación.
El otro parámetro es la resistencia a la extracción (Pullout ) que se calcula mediante la siguiente relación:

T_Pullout=2·L_e·σ’_v·f_b·tanδ

Para geosintéticos no tejidos:
f_b=tanδ/tanφ
Donde:

δ                 Representa  el ángulo de rozamiento entre el terreno y el refuerzo.
T_Pullout      Resistencia que moviliza un refuerzo anclado en una longitud Le al interior de la parte estable del terreno.
L_e                      Longitud de anclaje del refuerzo al interior de la parte estable.
f_b                Coeficiente de Pullout.
σ’_v              Tensión vertical, calculada a la profundidad media del tramo de refuerzo anclado al terreno.

A efectos de la comprobación, se elige el valor mínimo entre T_Allow y  T_Pullout, la verificación interna se satisface si la fuerza que transmite el refuerzo generada en la parte posterior del tramo reforzado no supera el valor de la T’.

Anclajes
Los anclajes, tirantes o clavos, son elementos estructurales capaces de sostener fuerzas de tracción gracias a una adecuada conexión con el suelo.
Los elementos que caracterizan un anclaje son:

• cabeza: indica el conjunto de elementos cuya función es transmitir la fuerza de tracción del anclaje a la estructura;
• cimentación: indica la parte del anclaje que realiza la conexión con el suelo, transmitiendo al mismo la fuerza de tracción del anclaje.

 

Bulbo completamente anclado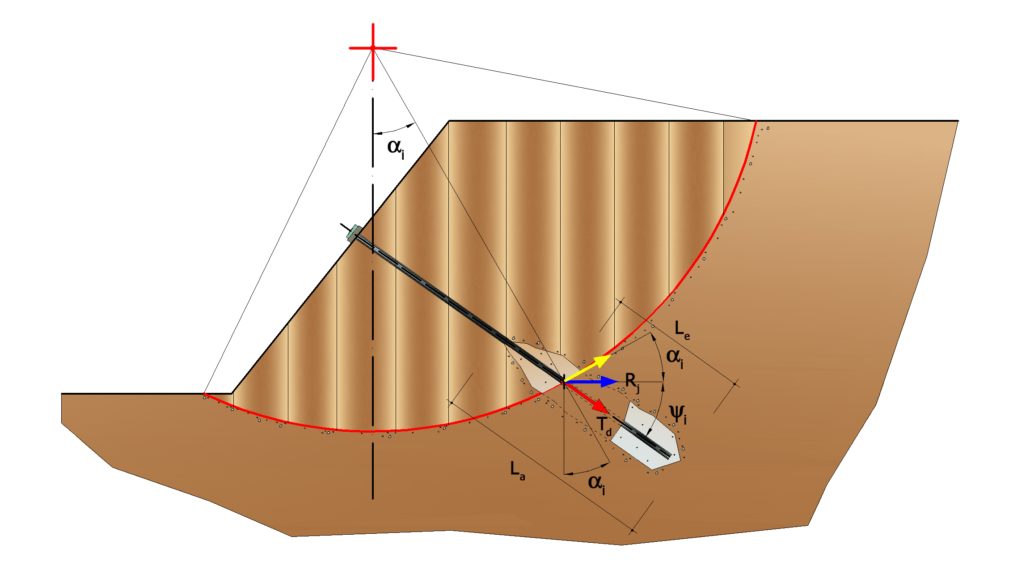

 

 

Bulbo parcialmente anclado

Las fórmulas que expresan la medida de seguridad a lo largo de una supuesta superficie de deslizamiento se verán modificadas con la presencia de anclajes (activos, pasivos y clavos) de la siguiente manera:

• con anclajes activos, su presencia deduce de las acciones (denominador);

FS=R_d/[E_d-Σ_i,jR_i,j·(1/cosα_i)]

• con anclajes pasivos y con clavos, su contribución se suma a las resistencias (numerador)

FS=[R_d+Σ_i,jR_i,j·(1/cosα_i)]/E_d

•  Con R_j se indica la resistencia del anclaje y se calcula mediante la siguiente expresión:

R_j=T_d·cosΨ_i·(1/i)·(Le/La)

donde:

T_d            resistencia de proyecto;
Ψ _i           inclinación del anclaje con respecto a la horizontal;anchor inclination relative to the horizontal;
i               intereje;
Le            longitud eficaz;
La            longitud de anclaje.

Los dos índices (i, j) de la sumatoria representan, respectivamente, la i-ésima rebanada y el j-ésimo anclaje interceptado por la superficie de deslizamiento de la i-ésima rebanada.

Extract of the technical report of SLOPE